1.4 A solução nos dias atuais
Contemporaneamente, a primeira contribuição importante para o problema foi dada por dois matemáticos: Yutaka Taniyama e Goro Shimura. A conjectura apresentada pelos dois serviu de base para solução definitiva do problema, infelizmente um dos matemáticos, Yutaka Taniyama, cometeu suicídio em 1958, adiando ainda mais o desenvolvimento da solução. O desenvolvimento dessa conjectura não foi intencionalmente feito para solucionar o Último Teorema de Fermat, mas foi o que acabou acontecendo. Interessante notar que vários matemáticos partiram da tentativa de solucionar o problema e acabaram fazendo contribuições importantes para outras áreas da matemática, sem intenção de fazê-lo, já no caso dos dois matemáticos citados, o fato ocorreu às avessas, o que demonstra a subjetividade do campo matemático, que se assemelha a uma forma de arte em que a inspiração é tão ou mais importante do que o trabalho metódico e racional, que geralmente está associado a matemática.
Com isso, mais uma característica interessante da matemática surge, que é a inter-relação entre as suas diversas subáreas, visto que o conhecimento produzido em um campo pode ser utilizado em aplicações de outros, e que o trabalho matemático, principalmente o de vanguarda, sempre terá uma aplicação, mesmo que seja insuspeita a princípio, pois quem imaginaria que o trabalho de dois estudantes do final do século XX poderia ser utilizado na solução de um dos problemas mais instigantes da história da matemática?
Observa-se dessa forma, que a pesquisa teórica é a semente de todo o desenvolvimento científico, e que a matemática como base de todas as ciências naturais, é o ferramental básico de toda pesquisa, sem tal ferramenta não seria possível abstrair a mente e criar conjecturas necessárias para desenvolver as soluções e técnicas modernas que transformam a vida de toda a humanidade. O senso comum poderia dizer que tais conjecturas são inúteis, desprovidas de qualquer utilidade prática, mas sem elas não nenhuma das técnicas modernas que desenvolvem a sociedade seriam possíveis. E mesmo a resolução de um problema tão teórico como o "Último Teorema de Fermat" está intimamente ligado a todo esse processo de crescimento da sociedade, visto que se observa nele a mesma essência necessária para o progresso da sociedade e da vida humana.
A conjectura feita pelos dois matemáticos diz que para cada equação elíptica há uma forma modular correspondente; a relevância dessa conjectura reside no fato de que se a mesma estiver correta ela poderia ser aplicada ao Último Teorema de Fermat provando a sua veracidade. Ou seja, para provar se o Último Teorema de Fermat era ou não verdadeiro, deveria se provar primeiro a conjectura Taniyama-Shimura, e foi exatamente isso que Andrew Wiles fez, como veremos no próximo capítulo.
Pelo que foi dito acima, percebe-se que não é possível desenvolver um trabalho em matemática ou em qualquer outra área, sem a contribuição de outros pesquisadores, sendo sempre necessário consultar outras pesquisas de modo a encontrar algo que possa ser útil, pois a pesquisa matemática não se faz isoladamente mas através do intercâmbio de idéias entre diversas pessoas e o estudo minucioso de pesquisadores já consagrados pela relevância de seus trabalhos.
No presente caso, sem a contribuição de Yutaka Taniyama e Goro Shimura dificilmente se teria chegado a uma resolução do problema, como de fato ocorreu alguns anos depois, demonstrando desse modo a importância do intercâmbio de idéias no mundo matemático.
II – A DEMONSTRAÇÃO DO TEOREMA
A solução definitiva do teorema se deve a Andrew Wiles, um professor da Universidade de Princeton, que iniciou seu interesse pelo problema ainda menino na biblioteca pública de sua cidade natal. Mas só a partir de 1986 é que começou realmente o trabalho de solucionar o teorema, o detalhe é que a sua pesquisa foi feita em segredo, talvez temendo a pressão que sofreria diante de um problema tão famoso e de difícil solução. Assim sendo, durante sete anos publicou outros trabalhos, afim de não despertar suspeitas sobre o seu verdadeiro objetivo, e apesar de não ser sua meta principal, estes trabalhos acabaram tendo grande relevância acadêmica, unificando e criando novas técnicas matemáticas.
Mas foi a partir da análise da conjectura Taniyama-Shimura que Andrew Wiles percebeu que o teorema poderia ser solucionado, porém a conjectura necessitava ser comprovada, ficou claro então na mente de Wiles que a solução do teorema dependeria da comprovação da conjectura, na verdade Wiles não demonstrou o Último Teorema de Fermat, mas a conjectura Taniyama-Shimura, sendo que esta levou a aquela.
Finalmente, no dia 23 de junho de 1993, em uma Conferência no Sir Isaac Newton Institute for Mathematical Sciences em Cambridge, Andrew Wiles, passados 356 anos desde a apresentação do teorema, faz o anúncio da descoberta de sua demonstração, para assombro de todos os presentes. Infelizmente havia uma pequena falha na sua demonstração, Wiles então se afasta por mais um ano, a fim de corrigir o erro e apresentar a nova demonstração reformulada.
Um detalhe deve ser lembrado nesse momento: para a maioria das pessoas, a matemática é uma ciência exata e perfeita, isso se deve a maneira como os professores, de modo geral, apresentam a matéria a seus alunos nas salas de aula, onde há sempre uma solução para cada problema e essas soluções se desenvolvem naturalmente sem percalços e nem dificuldades, pelos menos da maneira como são apresentadas, dando a impressão ao aluno que a dificuldade de encontrar uma solução para tais problemas é somente dele, que não tem capacidade para resolve-los. Esse tipo de matemática "higiênica" não deixa o aluno perceber que as dificuldades são normais na matemática e que até os grandes matemáticos se atolam na tentativa de solucionar os problemas. E que em matemática, tão importante quanto a solução de um problema é a maneira como se chega a ele, e é durante esse processo que ocorre a aprendizagem e não simplesmente obtendo uma resposta correta, que em si não significa nada, mas possui significado apenas se vier acompanhada de uma demonstração, pois é ai que reside o processo de aprendizado e onde algo de relevante pode ser notado. Como foi visto até aqui, várias contribuições foram feitas a matemática na tentativa de solucionar um problema, sem necessariamente atingir o objetivo principal.
Voltando à demonstração de Wiles, após a correção do erro detectado, foram necessários mais alguns meses para a apreciação da demonstração, que possuía cerca de 200 páginas, e após um período de suspense, a demonstração é finalmente aceita, sendo porém tão técnica que apenas alguns poucos no mundo todo eram capazes de compreendê-la, e Andrew Wiles (após receber um prêmio de 50 mil libras da Fundação Wolfskehl) entra para a história como o matemático que conseguiu demonstrar o teorema mais instigante e desafiador da história da matemática, que atravessou as épocas e ocupou a mente de grandes matemáticos ao longo desse período, “O Último Teorema de Fermat” foi definitivamente solucionado.
CONCLUSÃO
O objetivo deste trabalho foi tentar ressaltar a importância da pesquisa científica, e especificamente matemática, para a sociedade em geral, através de um apanhado histórico de fatos relevantes envolvendo o Último Teorema de Fermat. Com a apresentação desses fatos, tentou-se demonstrar que a matemática é um importante aliado para o benefício da sociedade visto que suas descobertas têm aplicação prática, mesmo que não seja imediata, ajudando a compreender fenômenos físicos, químicos, biológicos, etc... Que estão intimamente ligados ao nosso cotidiano, e do qual dependemos para viver e progredir como sociedade.
O Último Teorema de Fermat foi utilizado como exemplo a fim de mostrar como a matemática pode ser instigante e desafiadora, sendo uma ciência viva e dinâmica, e tentar desvincular dela a imagem de algo enfadonho e inútil; uma forma branda de tortura.
Deve ficar claro na mente de quem ler este trabalho, que não é a matemática enfadonha ou inútil, e se é essa a imagem que a pessoa tem, isso se deve a maneira como a matemática foi apresentada a ela.
Esperamos que se possa compreender a relevância da matemática para o desenvolvimento do mundo contemporâneo, não a culpando por prováveis dificuldades no sistema educativo.
BIBLIOGRAFIA:
• SINGH, Simon, O Último Teorema de Fermat, 1.ed. Rio de Janeiro: Record, 2002.
• FERMAT, Pierre, Arithmetica de Diofanto Contendo Observações por P. de Fermat, 1.ed. 1670.
• NASAR, Sylvia, Uma Mente Brilhante, 1.ed. Rio de Janeiro: Record, 2002.
• MARCONDES CÉSAR, Roberto, Resenha – O Último Teorema de Fermat. Disponível em http://www.ime.usp.br/. Acesso em : 29 mai. 2005 .
• MOREIRA CALAES, Antônio, Teorema de Fermat – Resumo Histórico. Disponível em http://www.powerline.com.br/~drcalaes/demo_do_teorema_port.htm, Acesso em : 29 mai. 2005.
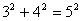 , mas existem outros exemplos:
, mas existem outros exemplos: 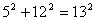 ,
, 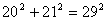 , e muitos outros. As ternas deste tipo, (3, 4, 5), (5, 12, 13), (20, 21, 29), são denominadas ternas pitagóricas. Por outro lado
, e muitos outros. As ternas deste tipo, (3, 4, 5), (5, 12, 13), (20, 21, 29), são denominadas ternas pitagóricas. Por outro lado 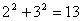 não é um quadrado. Portanto seguem questões como “Existem infinitas ternas pitagóricas?” e “ Se a resposta for positiva, poderemos encontrar uma fórmula que as descrevam em sua totalidade?”. Esses são alguns dos tipos de questões que a teoria dos números investiga.
não é um quadrado. Portanto seguem questões como “Existem infinitas ternas pitagóricas?” e “ Se a resposta for positiva, poderemos encontrar uma fórmula que as descrevam em sua totalidade?”. Esses são alguns dos tipos de questões que a teoria dos números investiga.




 é :
é :