"Seria possível dizer o que é a Matemática se esta fosse uma ciência morta. Mas a Matemática é, pelo contrário, uma ciência viva, que se encontra hoje, mais do que nunca, em rápido desenvolvimento, proliferando cada vez mais em novos ramos, que mudam não só a sua fisionomia, como até a sua essência."
Postagens mais visitadas
-
EVAPORAÇÃO : ocorre a qualquer temperatura e seu processo se dá de maneira lenta. Um exemplo são as roupas que se coloca a secar nos varais...
-
Dez minutos antes de colocar o bolo no forno, eu coloquei meu gato do lado de fora da casa. O bolo deve cozinhar por volta de 35 minutos, en... -
01. Por que utilizamos uma coluna de mercúrio e não de água para medir pressão? R: O mercúrio é ideal para o barômetro líquido pois a su...
-
Boa tarde, essa é simples, vejamos: o objetivo da pessoa é cozer as batatas em menos tempo ou evaporar a água? no caso é apenas cozer as ba...
-
Introdução: No estudo dos critérios de divisibilidade são dado regras que permitem verificar se um número é divisível por 2,3,5...
-
01. Um navio é feito de aço, que é muito mais denso do que a água. Porque os navios flutuam? R: Se o volume for bem razoável, a quantidad...
-
01. O dispositivo a seguir é composto de uma haste cilíndrica de metal e um disco de madeira, no qual existe um furo central. A haste passa ... -
Para garantir a segurança na utilização, a maior válvula comumente com um peso, serve para estabilizar a pressão interna que se forma durant...
-
O simples aspecto da mulher, revela que ela não é destinada nem aos grandes trabalhos intelectuais, nem aos grandes trabalhos materiais...
sexta-feira, 8 de outubro de 2010
terça-feira, 21 de setembro de 2010
sábado, 18 de setembro de 2010
sexta-feira, 17 de setembro de 2010
segunda-feira, 6 de setembro de 2010
sexta-feira, 27 de agosto de 2010
Mergulhando Fundo II (9º ano)
Mergulhando Fundo I (9º ano)
Mergulhando Fundo VIII (7º ano)
Mergulhando Fundo VII (7º ano)
Mergulhando Fundo I (8º ano)
Dez minutos antes de colocar o bolo no forno, eu coloquei meu gato do lado de fora da casa. O bolo deve cozinhar por volta de 35 minutos, então eu coloquei o despertador para tocar 35 minutos após colocar o bolo no forno. Imediatamente fiz um café para mim, o que me tomou 6 minutos. Três minutos antes de acabar de beber o café o gato entrou em casa. Isso foi 5 minutos antes do despertador tocar. O telefone tocou no meio do tempo entre eu acabar de fazer o café e quando o gato entrou em casa. Falei ao telefone por 5 minutos e desliguei. Eram 3h 59 min da tarde.
a) A que horas coloquei o gato fora de casa?
a) A que horas coloquei o gato fora de casa?
b) Quantos minutos depois de colocar o gato fora de casa, o despertador tocou?
c) Quanto tempo o gato estava fora de casa até o momento em que o telefone tocou?
Mergulhando Fundo VI (7º ano)
quinta-feira, 26 de agosto de 2010
Mergulhando Fundo V (7º ano)
Mergulhando Fundo IV (7º ano)
Mergulhando Fundo III (7º ano)
Mergulhando Fundo II (7º ano)
Mergulhando Fundo I (7º ano)
Sabendo que o livro foi escrito no século XVIII, quantos anos viveu Paulo?
terça-feira, 10 de agosto de 2010
Outras pérolas!
"A principal função da raiz é se enterrar."
"Ângulo é duas linhas que vão indo e se encontram."
"Triângulo são os filhos trigêmeos do ângulo."
"Circunferência é uma roda chata. Para a sua fabricação usamos o compasso."
"Tangente é quando a bola passa raspando no jogo de futebol. Ela também tem o nome de trave."
"Conjunto vazio é aquele em que os músicos não sabem nada de música."
"Um paralelepípedo é um animal cujos dois pés são paralelos."
"Um número concreto é um número que vemos a olho nu."
"Triângulo é quando duas pessoas gostam da mesma, como vemos nas novelas o dito chamado ‘triângulo amoroso’."
"Quando abre o ângulo é seno e quando fecha é cosseno porque cola no seno."
Gênio russo rejeita 'Nobel da Matemática'
O matemático russo Gregori Perelman, que resolveu um dos grandes enigmas da matemática, recusou o prêmio Fields Medal, considerado o Nobel da Matemática. A informação foi dada pela União Internacional Matemática. Perelman, de 40 anos, deveria receber uma das quatro medalhas entregues nesta terça-feira pelo rei Juan Carlos, da Espanha, durante o Congresso Mundial de Matemática, que está sendo realizado em Madri. Os outros três matemáticos que receberam o prêmio foram o francês Wenelin Werner, o australiano Terence Tao e o russo Andrei Okunkov. Conjectura Poincaré Perelman também é visto como um potencial vencedor do prêmio de US$ 1 milhão (cerca de R$ 2,1 milhões) do Clay Mathematics Institute, em Massachusetts, nos Estados Unidos, por ter resolvido o que o centro considera um entre os sete mais importantes problemas matemáticos do milênio. A instituição deve dar o prêmio ao matemático quando estiver convencida que sua resolução não tem falhas. Perelman resolveu a chamada Conjectura Poincaré, formulada pelo grande matemático francês Henri Poincaré em 1904. Para os não-iniciados é difícil entender até mesmo a formulação do problema. A Conjectura Poincaré é considerada uma das questões centrais da Topologia, uma área da matemática que estuda as propriedades geométricas de objetos que não mudam quando são distorcidos, esticados ou encolhidos. Durante um século, cientistas em todo o mundo tentaram resolvê-la. Perelman, que trabalhava no Instituto de Matemática Steklov, em São Petersburgo, resolveu o problema há três anos. 'Assunto esotérico' Também conhecido como Grisha, o matemático russo colocou sua descoberta na internet em novembro de 2002 e recusou-se a dar entrevistas, dizendo que qualquer publicidade seria prematura – ou seja, até que seu trabalho fosse examinado por outros matemáticos. Na época, o matemático Tomasz Mrowka, do Massachusetts Institute of Technology (MIT), disse: "Estamos desesperadamente tentando entender o que ele fez". Desde então, matemáticos de todo o mundo vêm analisando a resolução e até agora ninguém encontrou falhas. A resolução de Perelman tem profundas implicações para a ciência. Segundo especialistas, ela permite que se faça um catálogo de todas as formas tridimensionais possíveis no Universo, o que significa que poderíamos descrever a forma do próprio cosmos. Neste contexto, o desaparecimento – ou, para muitos, a reclusão voluntária – do genial Perelman intriga e fascina a comunidade internacional dos matemáticos. Em entrevista à BBC, o escritor de livros científicos Simon Singh tentou explicar o comportamento excêntrico do matemático. "Matemática Pura é um assunto tão esotérico que você faz por amor. Você não faz por dinheiro, por recompensas, por reconhecimento ou medalhas", diz Singh. Para o escritor, Perelman é um exemplo extremo desse tipo de comportamento. "Ele resolveu o problema. E não se deu ao trabalho nem de publicar (em uma revista científica) o seu trabalho. Porque do ponto de vista dele, o problema foi resolvido e isso é o que interessa." | |||||
Quem quer ser um milionário ?
Os Problemas do Prêmio Millenium são sete problemas matemáticos. Este projeto foi iniciado pelo Clay Mathematics Institute. Atualmente, seis desses problemas permanecem por resolver. A correta solução de cada problema resulta em um prêmio de um milhão de dólares para quem conseguir resolvê-lo.  Veja quais são: • P versus NP • A conjectura de Hodge • A conjectura de Poincaré (resolvido por Grigori Perelman) • A hipótese de Riemann • A existência de Yang-Mills e a falha na massa • A existência e suavidade de Navier-Stokes • A conjectura de Birch e Swinnerton-Dyer |
quarta-feira, 21 de julho de 2010
Porquê o terno se chama terno?
Terno, referindo-se a vestuário, designava o conjunto de três peças: calça, paletó e colete. Por este motivo que é chamado terno. Porém, hoje ele é constituído de duas peças: calça e paletó. |
terça-feira, 13 de julho de 2010
O quociente e a incógnita
O quociente e a incógnita
Millôr Fernandes
"Às folhas tantas do livro de matemática,
um quociente apaixonou-se um dia doidamente por uma incógnita.
Olhou-a com seu olhar inumerável e viu-a, do ápice à base.
Uma figura ímpar olhos rombóides, boca trapezóide,
corpo ortogonal, seios esferóides.
Fez da sua uma vida paralela a dela até que se encontraram no infinito.
"Quem és tu?" - indagou ele com ânsia radical.
"Eu sou a soma dos quadrados dos catetos,
mas pode me chamar de hipotenusa".
E de falarem descobriram que eram o que, em aritmética,
corresponde a almas irmãs, primos entre-si.
E assim se amaram ao quadrado da velocidade da luz
numa sexta potenciação traçando ao sabor do momento e da paixão retas,
curvas, círculos e linhas senoidais.
Nos jardins da quarta dimensão,
escandalizaram os ortodoxos das fórmulas euclidianas
e os exegetas do universo finito.
Romperam convenções Newtonianas e Pitagóricas e, enfim,
resolveram se casar, constituir um lar mais que um lar,
uma perpendicular.
Convidaram os padrinhos:
o poliedro e a bissetriz, e fizeram os planos, equações e diagramas para o futuro,
sonhando com uma felicicdade integral e diferencial.
E se casaram e tiveram uma secante e três cones muito engraçadinhos
e foram felizes até aquele dia em que tudo, afinal, vira monotonia.
Foi então que surgiu o máximo divisor comum,
frequentador de círculos concêntricos viciosos,
ofereceu-lhe, a ela, uma grandeza absoluta e reduziu-a a um denominador comum.
Ele, quociente percebeu que com ela não formava mais um todo, uma unidade.
Era o triângulo tanto chamado amoroso desse problema,
ele era a fração mais ordinária.
Mas foi então que Einstein descobriu a relatividade
e tudo que era espúrio passou a ser moralidade,
como, aliás, em qualquer Sociedade ..."
terça-feira, 8 de junho de 2010
Vencedor da promoção.
O vencedor da promoção desse último Bimestre foi: Lucas Sampaio, ele receberá seu premio assim que estiver disponivel o livro, já foi solicitado, estamos no aguardo...em breve mais promoções!!!
sexta-feira, 21 de maio de 2010
Desafio 8
Se eu leio 5 páginas por dia de um livro, eu termino de ler 16 dias antes do que se eu estivesse lendo 3 páginas por dia. Quantas páginas tem o livro?
a) 100
b) 110
c) 120
d) 130
e) 140
Esse é para iniciantes bons estudos e ótima diversão!!!
a) 100
b) 110
c) 120
d) 130
e) 140
Esse é para iniciantes bons estudos e ótima diversão!!!
quinta-feira, 13 de maio de 2010
Você sabe qual a origem da superstição em torno do número 13?
Você sabe qual a origem da superstição em torno do número 13? Na mitologia nórdica, encontramos uma lenda sobre o assunto. Odin, chefe de uma tribo asiática, estabeleceu na Escandinávia seu reino. Para administrá-lo, celebrar os rituais religiosos e predizer o futuro, Odin teria escolhido doze sábios, reunindo-os em um banquete no Valhalla, morada dos deuses. Loki, o deus do fogo, apareceu sem ser convidado e armou uma grande confusão. Como invejava a beleza radiante de Balder, deus do Sol e filho de Odin, fez com que Hodur, o deus cego, o assassinasse por engano. Daí veio a crendice de que 13 pessoas reunidas para um jantar é desgraça certa. Essa lenda é semelhante, ao episódio da Ultima Ceia de Cristo: Segundo alguns relatos, participaram dessa ceia sagrada os doze apóstolos e Cristo, num total de 13 pessoas. Também aí o final foi infeliz: a crucificação e morte de Cristo, numa sexta-feira. E mais. Na antiga numeração hebraica, os números eram representados por letras. A letra que indicava a quantidade treze era a mesma usada para a palavra morte. |
quarta-feira, 12 de maio de 2010
Quem descobriu o Teorema de Pitágoras?
A tradição matemática ocidental, durante longo tempo, atribuiu a descoberta deste teorema a Pitágoras. Pesquisas históricas mais recentes constataram que o teorema era conhecido pelos babilônios, cerca de 1500 a.C., portanto muito tempo antes de Pitágoras. Os chineses o conheciam talvez por volta de 1100 a.C. e os hindus provavelmente cerca de 500 a.C.
Referências
Boyer, C.B., História da Matemática. São Paulo, Editora Edgard Blücher, 1996.
Eves, H., Introdução à História da Matemática. Campinas, Editora da UNICAMP, 1995.
Boyer, C.B., História da Matemática. São Paulo, Editora Edgard Blücher, 1996.
Eves, H., Introdução à História da Matemática. Campinas, Editora da UNICAMP, 1995.
Você sabe o que é pentagrama?
Um pentagrama é uma estrela composta por cinco retas e que possui cinco pontas.  Podemos enxergá-la como uma estrela feita pela união dos pontos de um pentágono regular. Na língua portuguesa, pentagrama significa uma palavra com cinco letras. |
Quais são os anos Bissextos?
Um ano é bissexto quando ele é divisível por 4. Porém, existe uma exceção. Os anos que terminam por dois zeros serão bissextos se forem divisíveis por 400. Exemplo: 2012 é um ano bissexto. Pois 2012 / 4 = 503, ou seja, uma divisão exata. 1998 não é um ano bissexto, pois 1998 / 4 = 499,5, uma divisão inexata. 5000 não é um ano bissexto pois, apesar de ser divisível por 4, é um número terminado em 00 e não é divisível por 400. |
Você sabe fazer mágica com o calendário?
Peça a uma pessoa que, em um mês qualquer do calendário, ela delimite um “quadrado” 3 por 3, contendo 9 dias quaisquer. Veja o exemplo de uma escolha no calendário abaixo para o mês agosto de 2005.
Depois, peça que ela informe qual é a menor data do quadrado, e diga que com apenas essa data você irá descobrir a soma de todas as datas escolhidas. Para isso, você deve somar a menor data (no caso, 10) com 8 e multiplicar o resultado por 9. Ou seja, (10 + 8) x 9 = 18 x 9 = 162 (ou seja, 10 + 11 + 12 + 17 + 18 + 19 + 24 + 25 + 26 = 162). | |||||||||||||||||||||||||||||||||||||||||||||||||
Você sabe o que é Sudoku?
Sudoku é um game divertidíssimo e viciante, que está virando febre no mundo inteiro. O objetivo do jogo é completar um grid (colunas verticais e linhas horizontais), preenchendo os espaços vazios com números de 1 a 9. O segredo: o número não pode ser repetido na mesma coluna, linha ou bloco. Veja a seguir um exemplo de Sudoku, com sua respectiva solução: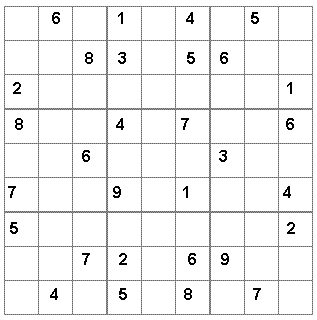 Solução:  |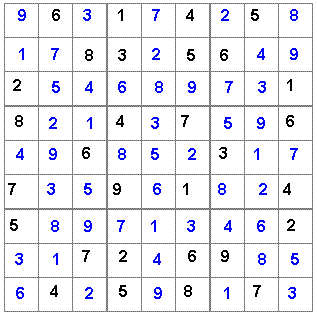
De onde originaram os sinais de adição e subtração?
O emprego regular do sinal + (mais) aparece na Aritmética Comercial de João Widman d'Eger, publicada em Leipzig em 1489. Entretanto, os sinais de mais e de menos não representavam a adição ou a subtração, ou os números positivos ou negativos, mas os excessos e os déficit em problemas de negócio (Cajori vol. 1, página 128). Os símbolos positivos e negativos vieram somente ter uso geral na Inglaterra depois que foram usados por Robert Recorde, em 1557. Todavia, já eram usados antes de aparecerem na escrita. Por exemplo: foram pintados em tambores para indicar se os tambores estavam cheios ou não. Os antigos matemáticos gregos, como se observa na obra de Diofanto, limitavam-se a indicar a adição juntapondo as parcelas - sistema que ainda hoje adotamos quando queremos indicar a soma de um número inteiro com uma fração. Como sinal de operação mais usavam os algebristas italianos a letra P, inicial da palavra latina plus. |
A fórmula é de Bhaskara mesmo?
Porém, problemas envolvendo equações do segundo grau já apareciam, há quase quatro mil anos, em textos escritos pelos babilônios. Esses textos possuiam uma receita (escrita em prosa, sem uso de símbolos), que ensinava como proceder para determinar as raízes.
Além disso, até o fim do século 16, não se usava uma fórmula para obter as raízes de uma equação do segundo grau, simplesmente porque não se representavam por letras os coeficientes de uma equação. Isso começou a ser feito a partir de François Viete, matemático francês que viveu de 1540 a 1603.
Logo, embora não se deva negar a importância e a riqueza da obra de Bhaskara, não é correto atribuir a ele a conhecida formula de resolução da equação do segundo grau.
|
Qual o dia da Matemática?
A Sociedade Brasileira de Educação Matemática (SBEM) elegeu o dia 6 de maio “DIA NACIONAL DA MATEMÁTICA”, em memória da data de nascimento de Júlio César de Mello e Souza, o MALBA TAHAN. Neste dia, fica a sugestão de promover, em todos os estados brasileiros, a realização de eventos comemorativos, com o objetivo de difundir a Matemática como área do conhecimento, sua História, possíveis relações com as demais áreas, e de colocar em discussão algumas crenças sobre o ensino atual de Matemática. |
terça-feira, 20 de abril de 2010
A teoria do números, a rainha da matemática
teoria dos números é o estudo dos números naturais ou inteiros positivos 1, 2, 3, 4,... e suas propriedades. O matemático Leopold Kronecker certa vez observou que, ao se tratar de matemática, Deus criou os números naturais e o resto é obra da humanidade. Contudo, os inteiros positivos representam, sem sombra de dúvida, a primeira criação matemática humana, e é difícil imaginar a humanidade destituída da habilidade de contar.
Embora os números naturais constituam, em um certo sentido, o sistema matemático mais elementar, o estudo de suas propriedades tem exercido grande fascínio na mente humana desde as mais remotas épocas da antiguidade, desafiando inúmeras gerações de matemáticos e leigos, que apreciam os seus enunciados simples e intrigantes, cujas demonstrações estão além de qualquer simplicidade.
Dentre os tesouros do antigo Egito se encontra o papiro Rhind descrevendo a matemática praticada no Egito há aproximadamente 2000 anos a.C.. Registros históricos mostram que os sumérios desenvolveram algum tipo de aritmética pois, por volta de 3500 a.C., possuíam um calendário e, por volta de 2500 a.C., desenvolveram um sistema numérico utilizando o número 60 como base. Os babilônios seguiram essa tradição e se tornaram exímios calculistas; tábuas de barro da Babilônia, datando de 2000 a.C., foram encontradas com elaboradas tabelas matemáticas. Ao final do terceiro milênio a.C. tábuas cuneiformes da Mesopotâmia mostravam que a Aritmética já era bastante sofisticada.
Os números foram utilizados nas transações comerciais por mais de 2000 anos até que se pensasse em estudá-los de forma sistemática. A primeira abordagem científica ao estudo dos números inteiros, isto é, a verdadeira origem da teoria dos números, é geralmente atribuída aos gregos. Por volta de 600 a.C. Pitágoras e seus discípulos fizeram vários estudos interessantes. Eles foram os primeiros a classificar os inteiros de várias maneiras:números pares, ímpares, primos, etc..
Na verdade não são exatamente os números naturais que exercem fascínio estético, místico e prático, mas as relações que eles estabelecem entre si. É dentro dessas relações profundas e sutis que se encontra a beleza, encanto e fascínio que os números exercem através das gerações.
A teoria dos números é a área da matemática cujo objetivo é descobrir e estabelecer as relações profundas e sutis que números de tipos diferentes guardam entre si. Por exemplo, considere os quadrados dos números naturais 1, 4, 9, 16, 25,... . Se tomarmos a soma de dois quadrados, eventualmente obteremos como resultado um outro quadrado. O exemplo mais famoso é: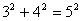 
, mas existem outros exemplos: 
, 
, e muitos outros. As ternas deste tipo, (3, 4, 5), (5, 12, 13), (20, 21, 29), são denominadas ternas pitagóricas. Por outro lado 
não é um quadrado. Portanto seguem questões como “Existem infinitas ternas pitagóricas?” e “ Se a resposta for positiva, poderemos encontrar uma fórmula que as descrevam em sua totalidade?”. Esses são alguns dos tipos de questões que a teoria dos números investiga.
, mas existem outros exemplos: 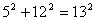, , 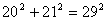e muitos outros. As ternas deste tipo, (3, 4, 5), (5, 12, 13), (20, 21, 29), são denominadas ternas pitagóricas. Por outro lado 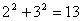não é um quadrado. Portanto seguem questões como “Existem infinitas ternas pitagóricas?” e “ Se a resposta for positiva, poderemos encontrar uma fórmula que as descrevam em sua totalidade?”. Esses são alguns dos tipos de questões que a teoria dos números investiga. A teoria dos números é povoada por uma variedade enorme de objetos: números primos, quadrados, ímpares e perfeitos; conjuntos dos números racionais, algébricos, e transcendentes, algumas funções analíticasbastante específicas tais como séries de Dirichlet e formas modulares; equações tais como a de Fermat e de Pell, curvas elípticas, códigos, alguns objetos geométricos tais como reticulados, feixes sobre Z e muitos outros que encontraremos em nossa jornada através da teoria dos números.
As Ternas Pitagóricas
A teoria dos números é a área da matemática que investiga relações profundas e sutis entre os números inteiros positivos. Pitágoras e seus seguidores ligaram tais números à geometria e, dessa forma, iniciou-se uma das vertentes mais bem sucedida da teoria dos números, a saber o binômio: aritmética e geometria. Por volta de 1700 AC foram encontradas, na Babilônia, tabelas contendo listas de ternas de números inteiros com a propriedade de que um dos números quando elevado ao quadrado era igual à soma dos quadrados dos outros dois. Como tais listas eram extensas, acredita-se que os Babilônios já possuíam um método sistemático de gerar tais ternas. Há registros históricos que comprovam a existência e uso de tais tabelas no Egito antigo.Considere os quadrados dos números naturais 1², 2², 3², 4², 5²,... . Se tomarmos a soma de dois quadrados, eventualmente obteremos como resultado um outro quadrado. O exemplo mais famoso desse fato é: 3²+4²=5², mas existem outros exemplos: 5²+12² = 13², 20²+21² = 29², e muitos outros. Contudo 2²+3² =13 não é um quadrado. Portanto, é natural perguntar se existe um número infinito de ternas Pitagóricas. A resposta é afirmativa e o motivo é muito simples: se (x, y, z) é uma terna Pitagórica, então ao multiplicá-la por um inteiro positivo c, obtemos (cx, cy, cz) que é uma nova terna Pitagórica, pois,
(cx)²+(cy)²= c²(x²+y²) = c²z² = (cz)².
Por outro lado essas ternas não são as mais interessantes e então definimos ternas primitivas, ou seja, aquelas em que a, b, e c não possuem fator comum e satisfazem à relação x²+y² = z².
(cx)²+(cy)²= c²(x²+y²) = c²z² = (cz)².
Por outro lado essas ternas não são as mais interessantes e então definimos ternas primitivas, ou seja, aquelas em que a, b, e c não possuem fator comum e satisfazem à relação x²+y² = z².
Por outro lado, os Pitagóricos estavam interessados nos triângulos retângulos cujos catetos têm comprimento inteiro x e y e o comprimento z da hipotenusa se relaciona com x e y de modo que z² = x²+y². Tal relação é o o famoso Teorema de Pitágoras. A procura de todos os inteiros positivos que satisfazem à identidade x²+y²=z² é equivalente ao problema de se determinar todos os triângulos retângulos cujos lados são inteiros.
Os Pitagóricos foram, por volta de 600 AC, os primeiros a dar um método de determinação de infinitas ternas desse tipo, hoje denominadas de ternas Pitagóricas. Utilizando uma notação atual descrevemos o método da seguinte maneira:
sejam x = n, y = 1(n²– 1), z = 1 (n² + 1)
onde n é um inteiro ímpar maior que 1; então a terna resultante (x, y, z) é uma terna Pitagórica onde z = y + 1. Observe alguns exemplos: 3² + 4² = 5², 5² + 12² = 13², 7² + 24² = 25², 9² + 40² = 41², 11² + 60² = 61². Observe que existem outras ternas além dessas: por exemplo, quando z = y + 2, ou seja, 8² + 15² = 17², 12² + 35² = 37², 16² + 63² = 99², 20² + 65² = 101². O filósofo Platão (430 – 349 AC) encontrou um outro método para determinar todas essas ternas, que em notação moderna são as fórmulas: x = 4n, y = 4n² – 1, z = 4n² +1. O matemático grego Tales de Mileto provocou uma mudança substancial no conhecimento quando transformou a matemática que até então era praticada como alguma forma de numerologia em uma ciência dedutiva. Por volta de 300 AC, quando Euclides publicou a coleção de 13 livros denominada Elementos, todos os fatos matemáticos apresentados foram demonstrados formalmente. No décimo livro, Euclides deu um método de obtenção de todas as ternas Pitagóricas. Apesar de não apresentar uma demonstração formal do seu método, Euclides obtinha todas as ternas. Utilizando-se a notação atual, o método consiste nas seguintes fórmulas:
x = t(a²-b²), y = 2tab, z = t(a²+b²)
onde t, a, e b, são inteiros positivos arbitrários tais que a>b, a e b não possuem fatores em comum, e se a é ímpar então b é par e vice-versa. Isso resolve completamente o problema natural de se saber quais são todas as ternas Pitagóricas.
sejam x = n, y = 1(n²– 1), z = 1 (n² + 1)
onde n é um inteiro ímpar maior que 1; então a terna resultante (x, y, z) é uma terna Pitagórica onde z = y + 1. Observe alguns exemplos: 3² + 4² = 5², 5² + 12² = 13², 7² + 24² = 25², 9² + 40² = 41², 11² + 60² = 61². Observe que existem outras ternas além dessas: por exemplo, quando z = y + 2, ou seja, 8² + 15² = 17², 12² + 35² = 37², 16² + 63² = 99², 20² + 65² = 101². O filósofo Platão (430 – 349 AC) encontrou um outro método para determinar todas essas ternas, que em notação moderna são as fórmulas: x = 4n, y = 4n² – 1, z = 4n² +1. O matemático grego Tales de Mileto provocou uma mudança substancial no conhecimento quando transformou a matemática que até então era praticada como alguma forma de numerologia em uma ciência dedutiva. Por volta de 300 AC, quando Euclides publicou a coleção de 13 livros denominada Elementos, todos os fatos matemáticos apresentados foram demonstrados formalmente. No décimo livro, Euclides deu um método de obtenção de todas as ternas Pitagóricas. Apesar de não apresentar uma demonstração formal do seu método, Euclides obtinha todas as ternas. Utilizando-se a notação atual, o método consiste nas seguintes fórmulas:
x = t(a²-b²), y = 2tab, z = t(a²+b²)
onde t, a, e b, são inteiros positivos arbitrários tais que a>b, a e b não possuem fatores em comum, e se a é ímpar então b é par e vice-versa. Isso resolve completamente o problema natural de se saber quais são todas as ternas Pitagóricas.
Assinar:
Postagens (Atom)