"Seria possível dizer o que é a Matemática se esta fosse uma ciência morta. Mas a Matemática é, pelo contrário, uma ciência viva, que se encontra hoje, mais do que nunca, em rápido desenvolvimento, proliferando cada vez mais em novos ramos, que mudam não só a sua fisionomia, como até a sua essência."
Postagens mais visitadas
-
EVAPORAÇÃO : ocorre a qualquer temperatura e seu processo se dá de maneira lenta. Um exemplo são as roupas que se coloca a secar nos varais...
-
Dez minutos antes de colocar o bolo no forno, eu coloquei meu gato do lado de fora da casa. O bolo deve cozinhar por volta de 35 minutos, en...
-
01. Por que utilizamos uma coluna de mercúrio e não de água para medir pressão? R: O mercúrio é ideal para o barômetro líquido pois a su...
-
Boa tarde, essa é simples, vejamos: o objetivo da pessoa é cozer as batatas em menos tempo ou evaporar a água? no caso é apenas cozer as ba...
-
Introdução: No estudo dos critérios de divisibilidade são dado regras que permitem verificar se um número é divisível por 2,3,5...
-
01. Um navio é feito de aço, que é muito mais denso do que a água. Porque os navios flutuam? R: Se o volume for bem razoável, a quantidad...
-
01. O dispositivo a seguir é composto de uma haste cilíndrica de metal e um disco de madeira, no qual existe um furo central. A haste passa ...
-
O simples aspecto da mulher, revela que ela não é destinada nem aos grandes trabalhos intelectuais, nem aos grandes trabalhos materiais...
-
Para garantir a segurança na utilização, a maior válvula comumente com um peso, serve para estabilizar a pressão interna que se forma durant...
sexta-feira, 27 de agosto de 2010
Mergulhando Fundo II (9º ano)
Duas partículas, A e B, percorrem uma circunferência de 120 metros de comprimento. A partícula A gasta 3 segundos menos que B, por estar animada com uma velocidade maior de 2 metros por segundo. Qual a velocidade de cada partícula?
Mergulhando Fundo I (9º ano)
Mergulhando Fundo VIII (7º ano)
Dois ciclistas, em sentidos opostos, se aproximaram em uma estrada reta, pedalando a 20 km/h. Quando estão distanciados 40 km, uma mosca pousa em uma das bicicletas, depois voa para outra. Então, a mosca fica indo e vindo entre as duas bicicletas, voando a 30 km/h, até que os dois ciclistas se encontram. Que distância percorreu a mosca?
Mergulhando Fundo VII (7º ano)
Ívina comprou um relógio no camelô e, após alguns dias de uso, passou a desconfiar de sua precisão. Ela percebeu, que o ponteiro das horas e dos minutos ficavam um sobre o outro a cada 65 minutos, medidos pelo aparelho do escritório, que é preciso. Quanto tempo o relógio de Ívina adianta por hora?
Mergulhando Fundo I (8º ano)
Dez minutos antes de colocar o bolo no forno, eu coloquei meu gato do lado de fora da casa. O bolo deve cozinhar por volta de 35 minutos, então eu coloquei o despertador para tocar 35 minutos após colocar o bolo no forno. Imediatamente fiz um café para mim, o que me tomou 6 minutos. Três minutos antes de acabar de beber o café o gato entrou em casa. Isso foi 5 minutos antes do despertador tocar. O telefone tocou no meio do tempo entre eu acabar de fazer o café e quando o gato entrou em casa. Falei ao telefone por 5 minutos e desliguei. Eram 3h 59 min da tarde.
a) A que horas coloquei o gato fora de casa?
a) A que horas coloquei o gato fora de casa?
b) Quantos minutos depois de colocar o gato fora de casa, o despertador tocou?
Mergulhando Fundo VI (7º ano)
Em um tanque há 4000 bolinhas de pingue-pongue. Um garoto começou a retirar as bolinhas, uma por uma, sempre com a mesma velocidade, quando eram 10 horas. Após 6 horas, havia no tanque 3520 bolinhas. Se o garoto continuasse no mesmo ritmo, quando o tanque ficaria com 2000 bolinhas?
quinta-feira, 26 de agosto de 2010
Mergulhando Fundo V (7º ano)
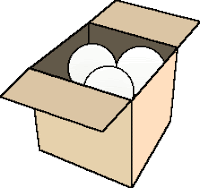
Em uma caixa quadrada há 4 bolas brancas e 2 bolas pretas, e numa caixa redonda há 6 bolas, todas pretas. Paula quer que tanto na caixa quadrada quanto na redonda a fração entre a quantidade de bolas brancas e o total de bolas em cada caixa seja a mesma. Quantas bolas brancas Paula precisa tirar da caixa quadrada e passar para a caixa redonda?
Mergulhando Fundo IV (7º ano)
Se leio 5 páginas, por dia, de um livro, eu termino de ler 16 dias antes do que se eu estivesse lendo 3 páginas por dia. Quantas páginas tem o livro?
Mergulhando Fundo III (7º ano)
Uma professora distribuiu 286 bombons igualmente entre seus alunos do 6º ano. No dia seguinte, ela distribuiu outros 286 bombons, também igualmente, entre seus alunos do 7º ano. Os alunos do 7º ano reclamaram que cada um deles recebeu 2 bombons a menos que os alunos do 6º ano. Quantos alunos a professora tem no 7º ano?
Mergulhando Fundo II (7º ano)
Uma cidade ainda não tem iluminação elétrica e todos usam velas à noite. Na casa de José usa-se uma vela por noite, sem queimá-la totalmente: com os tocos de quatro destas velas, é possível fazer uma nova vela. Durante Quantas noites José poderá iluminar sua casa com 43 velas?
Mergulhando Fundo I (7º ano)
Ao abrir um livro um antropólogo encontrou a seguinte mensagem:" meu nome é Paulo. O ano que nasci era um cubo perfeito. O ano em que morri, um quadrado perfeito. O quanto vivi também era um quadrado perfeito."
Sabendo que o livro foi escrito no século XVIII, quantos anos viveu Paulo?
Sabendo que o livro foi escrito no século XVIII, quantos anos viveu Paulo?
terça-feira, 10 de agosto de 2010
Pérola do apelador...kkkkkkkkkkk!!!!!
Outras pérolas!
"A principal função da raiz é se enterrar."
"Ângulo é duas linhas que vão indo e se encontram."
"Triângulo são os filhos trigêmeos do ângulo."
"Circunferência é uma roda chata. Para a sua fabricação usamos o compasso."
"Tangente é quando a bola passa raspando no jogo de futebol. Ela também tem o nome de trave."
"Conjunto vazio é aquele em que os músicos não sabem nada de música."
"Um paralelepípedo é um animal cujos dois pés são paralelos."
"Um número concreto é um número que vemos a olho nu."
"Triângulo é quando duas pessoas gostam da mesma, como vemos nas novelas o dito chamado ‘triângulo amoroso’."
"Quando abre o ângulo é seno e quando fecha é cosseno porque cola no seno."
Pérola da Raiz!
Pérola da Expansão!
Pérola do Limite!

Pérola do descanso!

Pérola do seno!
Gênio russo rejeita 'Nobel da Matemática'
O matemático russo Gregori Perelman, que resolveu um dos grandes enigmas da matemática, recusou o prêmio Fields Medal, considerado o Nobel da Matemática. A informação foi dada pela União Internacional Matemática. Perelman, de 40 anos, deveria receber uma das quatro medalhas entregues nesta terça-feira pelo rei Juan Carlos, da Espanha, durante o Congresso Mundial de Matemática, que está sendo realizado em Madri. Os outros três matemáticos que receberam o prêmio foram o francês Wenelin Werner, o australiano Terence Tao e o russo Andrei Okunkov. Conjectura Poincaré Perelman também é visto como um potencial vencedor do prêmio de US$ 1 milhão (cerca de R$ 2,1 milhões) do Clay Mathematics Institute, em Massachusetts, nos Estados Unidos, por ter resolvido o que o centro considera um entre os sete mais importantes problemas matemáticos do milênio. A instituição deve dar o prêmio ao matemático quando estiver convencida que sua resolução não tem falhas. Perelman resolveu a chamada Conjectura Poincaré, formulada pelo grande matemático francês Henri Poincaré em 1904. Para os não-iniciados é difícil entender até mesmo a formulação do problema. A Conjectura Poincaré é considerada uma das questões centrais da Topologia, uma área da matemática que estuda as propriedades geométricas de objetos que não mudam quando são distorcidos, esticados ou encolhidos. Durante um século, cientistas em todo o mundo tentaram resolvê-la. Perelman, que trabalhava no Instituto de Matemática Steklov, em São Petersburgo, resolveu o problema há três anos. 'Assunto esotérico' Também conhecido como Grisha, o matemático russo colocou sua descoberta na internet em novembro de 2002 e recusou-se a dar entrevistas, dizendo que qualquer publicidade seria prematura – ou seja, até que seu trabalho fosse examinado por outros matemáticos. Na época, o matemático Tomasz Mrowka, do Massachusetts Institute of Technology (MIT), disse: "Estamos desesperadamente tentando entender o que ele fez". Desde então, matemáticos de todo o mundo vêm analisando a resolução e até agora ninguém encontrou falhas. A resolução de Perelman tem profundas implicações para a ciência. Segundo especialistas, ela permite que se faça um catálogo de todas as formas tridimensionais possíveis no Universo, o que significa que poderíamos descrever a forma do próprio cosmos. Neste contexto, o desaparecimento – ou, para muitos, a reclusão voluntária – do genial Perelman intriga e fascina a comunidade internacional dos matemáticos. Em entrevista à BBC, o escritor de livros científicos Simon Singh tentou explicar o comportamento excêntrico do matemático. "Matemática Pura é um assunto tão esotérico que você faz por amor. Você não faz por dinheiro, por recompensas, por reconhecimento ou medalhas", diz Singh. Para o escritor, Perelman é um exemplo extremo desse tipo de comportamento. "Ele resolveu o problema. E não se deu ao trabalho nem de publicar (em uma revista científica) o seu trabalho. Porque do ponto de vista dele, o problema foi resolvido e isso é o que interessa." | |||||
Quem quer ser um milionário ?
Os Problemas do Prêmio Millenium são sete problemas matemáticos. Este projeto foi iniciado pelo Clay Mathematics Institute. Atualmente, seis desses problemas permanecem por resolver. A correta solução de cada problema resulta em um prêmio de um milhão de dólares para quem conseguir resolvê-lo.  Veja quais são: • P versus NP • A conjectura de Hodge • A conjectura de Poincaré (resolvido por Grigori Perelman) • A hipótese de Riemann • A existência de Yang-Mills e a falha na massa • A existência e suavidade de Navier-Stokes • A conjectura de Birch e Swinnerton-Dyer |
Assinar:
Postagens (Atom)